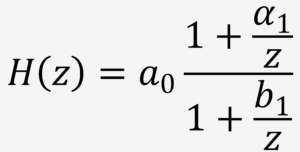均衡和濾波

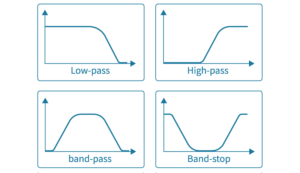
均衡器（Equalizer，一般簡稱EQ）的功能是提升（boost）或衰減（attenuate）特定頻率範圍。 例如說，他可以提升低頻量感，或是減弱幾根高頻陡峭的尖點（peak），或是彌補常見的喇叭中頻谷（mid frequency dip）。 EQ有分類比（analogue），也有數位（digital），一般和濾波（filter）一起進行調音。 EQ可能針對某頻點或是較狹窄的頻段來調音，來塑造出目標頻率響應曲線（target curve）； 另一方面，濾波通常針對更寬的頻段進行強化或衰減，例如低通濾波器（Low-Pass Filter；LPF）、高通濾波器（High-Pass Filter；HPF）、帶通濾波器（Band-Pass Filter；BPF）和帶阻濾波器（Band-Stop Filter；BSF）。

以下範例是利用軟體EQ調音，來改變喇叭的頻響曲線

  • 擇某喇叭單體量測頻率響應，發現其中低頻量感不足。
  • 以EQ調升中低頻。
  • 調整EQ前後頻率響應曲線比對： 拉升200hZ～1khz使中低頻音壓提升，進而使曲線更平坦。如下圖，紅色為未EQ前，綠色為EQ後。

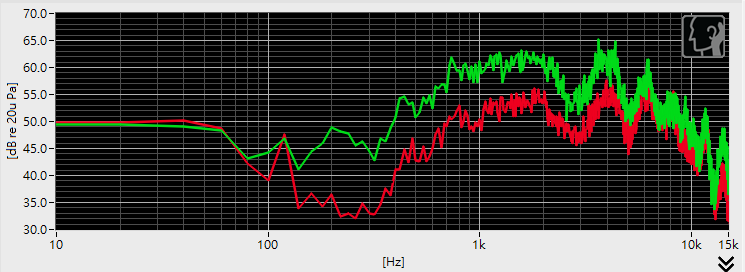
一般電聲單體的調音EQ，用階數較低的EQ即可達到

 

。考慮轉換函數（transfer function），他的極點（pole）就是讓H（s）變成無限大的s值，也就是X（s）的根（root），以p1, p2, p3…表達。他的零點（zero） 就是讓H（s）變成零的s值，也就是Y（s）的根，以z1, z2, z3…表達。在s平面上，H（s）的絕對值就是s平面起伏不定的面。在s平面的零點部分，可以看到H（s）變成0，視覺上是貼齊s平面。反觀在s平面的pole部分，H（s）會變成無限大。極點和零點都稱為系統的臨界頻率。

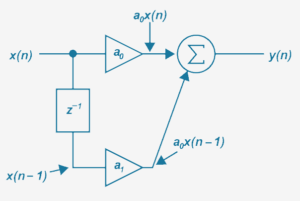
常見的最簡單濾波為1階前饋濾波( 1st order feed-forward)。 其方塊圖（block diagram）如下，並且表達式為 . 數位上，Z-1­­ 就是一個延遲（delay）， 可以透過Z 轉換相乘和 ejwt­ 等方式來表達複數和轉換函數的部分，. ­因為單純用三角函數來表示，在角度計算上很麻煩，而用z、e來計算就是相乘和相除即可，因為指數部分會變成相加和相減，較為方便。關鍵是如何把複數的概念對應到這些轉換函數和濾波等應用。 

舉例而言，時間 t 若延遲n 秒，就會從f（t）變成f（t-n）。知指數表示法為ejwt­. ­T而延遲n秒的就是ejw(t-n)。 要算出這個只需要單純e-jwt­-jwn即可。 以1.階前饋濾波為例，他的原本表達式為，我們現在轉成在數位離散的。 知x（nT）為 ejwnt，可替換為。 最後得 。 故方塊圖可表示為以下：

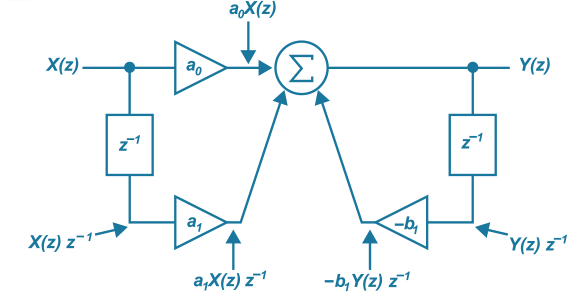
由於eejw的表示較為繁瑣，故我們把它用z轉換的z代替。因此得  。 可比對出乘以z-1 就是把訊號延遲1秒， 乘以z-n­­就是把訊號延遲n秒。 也就是假設x（n）=X（z），則x（n-1）=X（z） z-1。

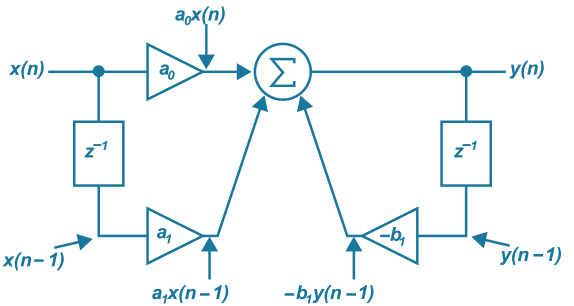
常見的濾波EQ是所謂的擱架式濾波（shelving filter）。 當反饋（feedback）和前饋結合在一起時，最簡單的形式就是1.階反饋前饋濾波（1st order feed forward-feedback filter）。

由定義知。 取z轉換並整理成 。 整理得。 故有 可知這個有1個zero當z=（-a1；有1個pole當z=（-b­1­）。