EQ and Filter

An equalizer (EQ) is a device that boosts or attenuates specific frequency ranges. For example, it can enhance the bass response or reduce sharp peaks in high frequencies, or compensate for mid-frequency dips commonly found in speakers. EQ can be classified as analog or digital and is usually used in conjunction with filtering. EQ can be used to shape the target frequency response curve by adjusting specific frequency points or narrower frequency bands. On the other hand, filters typically enhance or attenuate wider frequency ranges, such as low-pass filters (LPF), high-pass filters (HPF), band-pass filters (BPF), and band-stop filters (BSF).

The following example demonstrates using software EQ to modify the frequency response curve of a speaker.

  • We observe that the item lacks some lower and mid frequency energy.  
  • We choose to implement EQ especially on these bandwidths.
  • A comparison of the before-and-after frequency response, with the red line referring to the “before” and green line referring to the “after”. It shows that the lower to mid frequency band, such as 200hz~1khz, improves in magnitude after EQ.

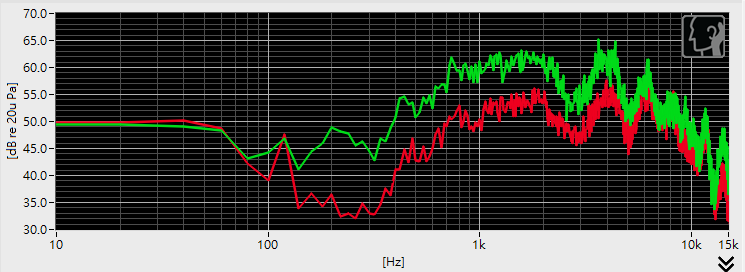
It’s possible to achieve good EQ results just by applying very few order filters.

 

Consider a transfer function in the form of, its poles are the s value that render H(s) infinitely big. The values are the roots of X(s), and are defined as p1, p2, p3….etc. On the other hand, its poles are the s values that render H(s) zero. The values are the roots of Y(s), and are defined z1, z2, z3…etc. On the s plane, zeros manifest themselves as lying flat on the s plane, while poles reach infinity and are portrayed as peaking hills. Poles and zeros are termed critical frequencies of the transfer function system.

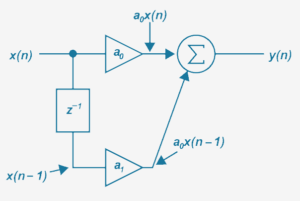
One of the simplest filters is the 1st order feed-forward one. Its block diagram is shown below and is expressed as . In the digital domain, Z-1­­ represents a delay. This symbol can be manipulated by Z transform into ejwt­. ­This is a convenient way to describe and operate with complex numbers, compared to the trigonometric functions. 

For example, one can delay the time t by n seconds, i.e. changing from f(t) to f(t-n), conveniently in the form of ejwt­. ­This is because the answer is an easy ejw(t-n). It’s clear that we only have to multiply by ­e-jwn­ to complete the calculation. In the case of 1st order feed forward filter, given its formula , it’s possible to rewrite it in discrete, digital domain: . Acknowledging x(nT) as ejwnt, we further rewrite the formula as . Finally we reach at the expression, . In this way, the block diagram can be shown as below:

As the expression of ejw is inefficient to manipulate, we replace this term with z, and rewrite it based on Z transform, and we now have . It’s clear that by multiplying z-1 we are essentially delaying the signal chain by one second. Apparently, multiplying z-1­­ corresponds to delaying the signal by n seconds. In other words, x(n)=X(z), and x(n-1)=X(z) z-1.

Some common EQ and filters include the shelving filter. When we combine feedback and feed forward filter, we have a 1st order feed forward-feedback filter.

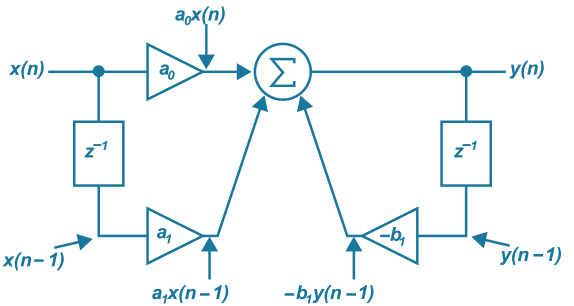
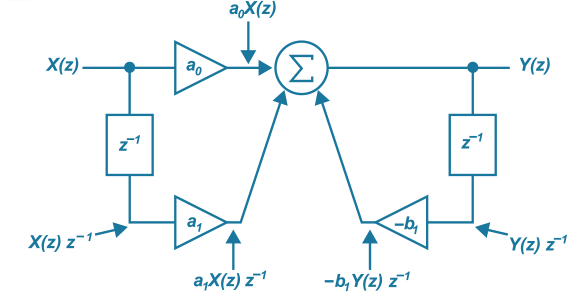
According to the given definition, we have. Taking the Z-transform and rearranging, we get . Simplifying further, we obtain. Therefore, we have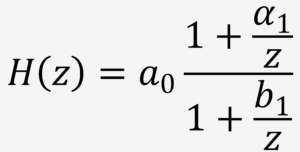. It can be observed that this transfer function has 1 zero at z = z=（-a1） and 1 pole atz=（-b­1­）.